Inhalt Splitter Dialog Betrifft Fundgrube Unterwegs Hörbar ?? EDV Links Datenschutz Impressum Suche
Kopfsplitter
EDV
Der Computer rechnet I
aktualisiert am 8.5.2022
Eine der elementarsten Aufgaben des Computers ist das Rechnen. Nicht von ungefähr bedeutet das Wort "compute" übersetzt "rechnen". Und rechnen kann er. Fehlerlos und blitzschnell. Das kennen Sie sicher von Ihrem Taschenrechner.
Wenn wir Menschen rechnen, gehen wir anders vor als ein Computer. Da wir denken können, erfassen wir zunächst eine Aufgabe als Ganzes und entscheiden dann, welchen Lösungsweg wir wählen.
Bei der Addition von 189 + 167 gibt es bestimmt 5 verschiedene Möglichkeiten, die Aufgabe im Kopf zu lösen. Wir entscheiden intuitiv und jeder für sich, welches die leichteste (und schnellste) wäre. Eventuell rechen wir sogar schriftlich. Bei der Addition von 100 + 100 gibt's dagegen nicht viel zu überlegen. Kein Mensch würde dafür Papier und Stift zur Hand nehmen.
Ein Computer kann nicht denken. Er braucht ein eindeutiges Schema, welches auf jeden Fall das richtige Ergebnis liefert, unabhängig davon, ob auch ein kürzerer Weg dorthin gewählt werden könnte. Die Geschwindigkeit, mit der die Maschine 100 + 100 addiert, ist daher dieselbe wie für 189 + 167.
Aber wie schafft er das mit nur 2 Zahlen, mit 0 und 1?
In den schon besprochenen Zeichensätzen kamen ja auch Zahlen vor. Die 1 z. B. hat die Code-Nr. 49. Aber das ist eben ein Zeichen wie in einer Telefon- oder Straßennummer. Kein Mensch rechnet mit Telefonnummern. Auch ein Computer schafft das nicht. Sonst könnte er auch mit "Y" oder "m" rechnen.
Es gibt also einen Unterschied zwischen dem Zeichen "1" und der Zahl 1. In einem Textverarbeitungsprogramm codiert der Computer das Zeichen "1" mit der Bitfolge 00110001. In einem Rechenprogramm z.B. wird die Zahl 1 mit 00000001 codiert. Der Unterschied liegt aber nicht nur in einem anderen Bitmuster.
Nehmen wir jetzt mal die 2 Zeichen "10" und die zweistellige Zahl 10. Für die Zeichen sind 2 Bytes notwendig (00110001 für "1" und 00110000 für "0"). Die Zahl 10 hingegen wird mit nur einem Byte codiert, nämlich mit 00001010. In einem Byte haben wir ja Platz für 256 Kombinationen. Daher wird für die Zahlen von 0 bis 255 (siehe oben) nur ein Byte benötigt. Alles andere wäre Verschwendung von Speicherplatz und Rechnerzeit. Als Zeichen wären bis zu 3 Bytes erforderlich.
Kleiner Einschub: Bei Datenbanken wird die Unterscheidung von Zeichen und Zahlen noch klarer. Dort werden nämlich die Eigenschaften der Feldinhalte vorher festgelegt. Wenn ein Feld als "numerisch" deklariert wird, dann werden Sie es nicht schaffen, einen Buchstaben darin einzugeben. Umgekehrt können Sie zwar eine 10 in ein Zeichen-Feld eingeben. Aber das sind für den Computer eben die beiden Zeichen "1" und "0". Es ist nicht die Zahl 10. Wie schon gesagt: Auch ein Computer kann nicht mit Zeichen rechnen.
Jetzt mal eine auszugsweise Gegenüberstellung des dualen und dezimalen Zahlensystems:
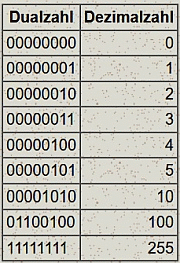
Auffällig ist die Bitfolge der Ziffer 2. Wir nehmen wahrscheinlich hinten eine 10 (Zehn) wahr. Aber das ist kein duales Denken. Wir müssen Eins-Null lesen. Wir werden gleich noch sehen, warum die 10 logisch ist und nicht eine 11 (also 2 Einsen).